Big O Notation in Computer Science
Big O notation is a common means of evaluating algorithm performance in terms of a parameter.For instance, if you say that a particular algorithm is O(n) it means that its runtime grows at the same rate as the parameter n.
If you say that a particular algorithm is O(n2) it means that its runtime grows at the same rate as the square of the parameter n. If you say that a particular algorithm is O(n!) it means that its execution time grows at the same rate as the factorial of the parameter n. You can learn the details of big O (and the related little o) notation in any standard data structures and algorithms text. However, since big O notation does not really work well as a measure of most design patterns, it will not be used in this course.
If you say that a particular algorithm is O(n2) it means that its runtime grows at the same rate as the square of the parameter n. If you say that a particular algorithm is O(n!) it means that its execution time grows at the same rate as the factorial of the parameter n. You can learn the details of big O (and the related little o) notation in any standard data structures and algorithms text. However, since big O notation does not really work well as a measure of most design patterns, it will not be used in this course.
Algorithm Performance and Case analysis of Runtime
Although developed as a part of pure mathematics, this notation is now frequently also used in the analysis of algorithms to describe an algorithm's usage of computational resources. These are described as
- the worst case or
- average case running time or
- memory usage of an algorithm
Big O notation
Big O notation is a theoretical measurement of the execution of an algorithm. It considers time, memory and problem size. It helps to analyze the programming code with different types of performance.
That is
Big O measure of asymptotic complexity: The complexity analysis helps to measure the performance of any algorithm irrespective of input size.
- best case,
- average case and
- worst case analysis.
Big O measure of asymptotic complexity: The complexity analysis helps to measure the performance of any algorithm irrespective of input size.
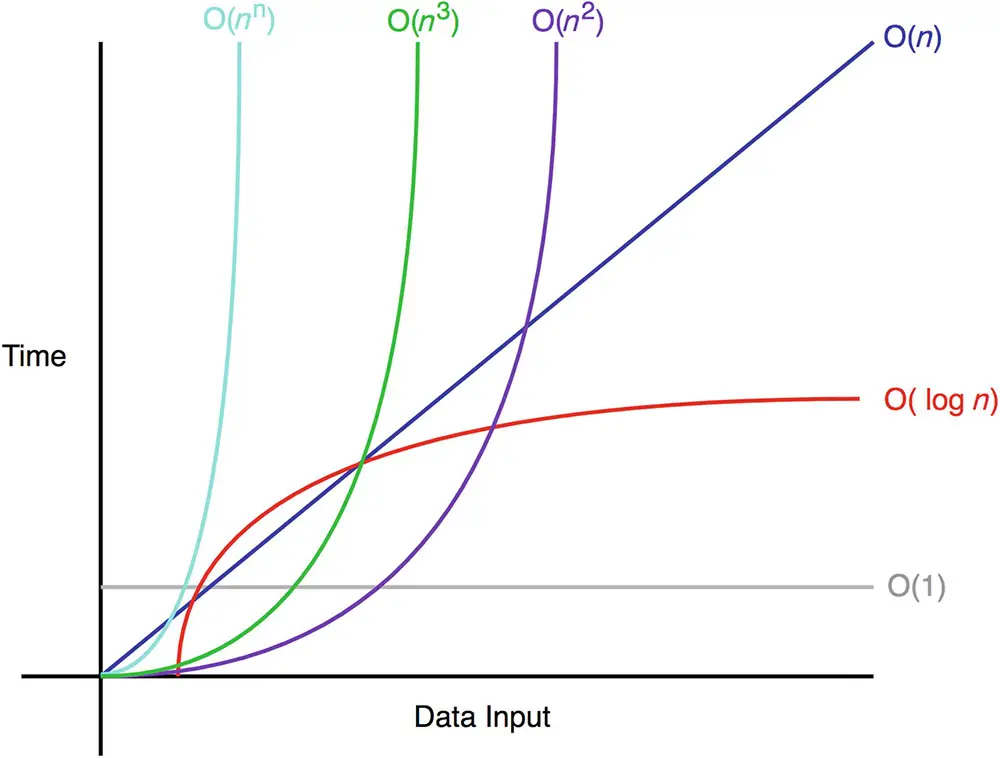
Algorithm performance
Algorithm efficiency is described in terms of 1) time and 2) space. The time efficiency is calculated using CPU utilization. The space efficiency is calculated using memory and disk usage of an algorithm. The developer should know the difference between performance and complexity. The complexity analysis does not depend on any computer resource. It may change based on the input size.
The algorithm performance is machine independent and does not depend on any other factors. The following table explains the various run times.
| Performance | Name | Description |
|---|---|---|
| O(1) | Constant | Does not depend on the size of the input |
| O(log(N)) | Logarithmic | Commonly found in operations on binary trees |
| O(N) | Linear | Running time increases linearly with the size of the input |
| O(N log(N)) | Super linear | Not allowed prior assumptions on the input |
| O(N^2) | Quadratic | Comparison-based sorting algorithms are quadratic |
| O(N^3) | Cubic | Naive multiplication of two N×N matrices |
| O(N^c) | Polynomial | Polynomial expression in the size of the input for the algorithm |
| O(C^N) | Exponential | Exponential time algorithms on a deterministic Turing machine form the complexity |
| O(N!) | Factorial | All the permutation of a list |
Algorithm Analysis
Algorithm analysis should be based in a machine independent manner. The RAM model is the memory model analysis which measures the run time by counting the number of steps involved for computing the algorithm.
It may be different based on the input size. But, the algorithm analysis does not depend on the type of computer.
The worst case analysis helps the algorithm behavior in worst case scenarios and is helpful in understanding the algorithm performance. Big oh notation simplifies the algorithm analysis by providing the simple questions to help understand the algorithm performance. Big o notation simplifies the comparison of algorithms.
The worst case analysis helps the algorithm behavior in worst case scenarios and is helpful in understanding the algorithm performance. Big oh notation simplifies the algorithm analysis by providing the simple questions to help understand the algorithm performance. Big o notation simplifies the comparison of algorithms.
N! >> C^N >> N^3 >> N^2 >> N log N >> N >> log N >> 1
Analysis Types
The algorithm complexity can be best, average or worst case analysis. The algorithm analysis can be expressed using Big O notation. Best, worst, and average cases of a given algorithm express what the resource usage is at least, at most and on average, respectively.
- Best case: Best-case performance is used in computer science to describe an algorithm’s behavior under optimal conditions. Example sort the array of items which are already sorted
- Worst case: Worst case performance is used to analyze the algorithm behavior under worst case input and least possible to solve the problem. It determines when the algorithm will perform worst for the given inputs.
- Average case: Average case performance is measured using the average optimal conditions to solve the problem. Example: sort partially sorted items using insertion sort
Amortized analysis:
Amortized analysis is a method for analyzing a given algorithm's time complexity.
It analyzes resource usage including
Amortized worst-case provides a guaranteed upper limit on the running time.
It examines how an algorithm will perform in practice or on average. The amortized cost of N operations is the total cost of the operations divided by N.
If the developer pushes or pops operations on a stack, it takes O(1) time.
If the stack is full, the stack doubles the array size, copies the old elements to the new array and requires more time. The developer can amortize the cost over the previous operations.
It analyzes resource usage including
- time and
- memory
Amortized worst-case provides a guaranteed upper limit on the running time.
It examines how an algorithm will perform in practice or on average. The amortized cost of N operations is the total cost of the operations divided by N.
If the developer pushes or pops operations on a stack, it takes O(1) time.
If the stack is full, the stack doubles the array size, copies the old elements to the new array and requires more time. The developer can amortize the cost over the previous operations.
Determine complexities
The algorithm complexity ignores the constant value in algorithm analysis.
If the algorithm takes, n^2+13n+43 time to calculate all the steps, the algorithm analysis ignores all the constants and takes a time of O(n^2).
If the algorithm takes, n^2+13n+43 time to calculate all the steps, the algorithm analysis ignores all the constants and takes a time of O(n^2).
Simple statement
The simple statement takes O(1) time.
int x= n + 13;
if condition
The best case O(1), worst case O(n)if( n> 12){
...
}else{
..
..
}
for/while loops
A loop takes N time to complete and has a runtime of O(n).for(int i=0;i<n;i++){
..
..
}
Nested loops
If the nested lops contains M and N size, the cost is O(MN)for(int i=0;i<n;i++){
for(int i=0;i<m;i++){
..
..
}
}
If you are preparing for an algorithm interview, you should understand algorithm analysis. If the interviewer asks about a problem which involves a data structure and algorithm, they will expect you to analyze the code based on complexity analysis. So, the candidate must understand the algorithm in terms of
- best,
- average and
- worst case
Ad Data Structures and Algorithms